![[알고리즘] (동적 계획법, DP) 가장 긴 증가하는 부분 수열, LIS(최종본)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fb3xap5%2FbtsA7ukEpjT%2FAAAAAAAAAAAAAAAAAAAAANJFJQUK0C99V51MHKMHFJBBvi5gFjYbMI2Pf9esL7SB%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3Ds83p%252F89WeHbnvaGtj3Yh8b4dHxU%253D)

1. 가장 긴 증가하는 부분 수열(LIS)이란?
증가하는 부분 수열을 중에서 길이가 가장 긴 수열을 말한다. 영어로는 줄여서 LIS(Longest Increasing Subsequence)라고 한다. 이때 부분수열의 원소들은 주어진 원래의 배열처럼 이어져 있지 않아도 된다는 특징이 있다.
예를 들어 다음과같은 수열 S(n)을 보자.
S(n) = {10, 20, 10, 30, 20, 50}
수열 S(n)에 대하여 다음과 같이 총 5개의 증가하는 부분 수열을 만들 수 있다.
{10, 20, 30, 50}
{20, 30, 50}
{10, 30, 50}
{30, 50}
{20, 50}
이 중에서 LIS는 {10, 20, 30, 50}이 되는 것이다.
부분 수열 문제는 배낭 문제(knapsack problem)의 특수한 경우이기도 하며 여러 종류가 있다. 또한 컴퓨터 과학과 수학의 분야에서 많이 연구되는 주제이기도 하다. 이 페이지에서는 LIS를 구하는 세 가지 알고리즘에 대해 알아보고 각각의 알고리즘을 분석해보며 예제를 소개한다.
2. LIS를 구하는 알고리즘
원래 주어진 수열을 S라고 하자.
S(n) = {10, 20, 10, 30, 20, 50}
LIS를 구하는 방법에는 크게 세 가지가 존재한다.
1) 완전 탐색(Brute Force) LIS 알고리즘
아이디어
앞의 예시에서 LIS가 만들어지는 과정을 보면 규칙이 보인다.
pivot을 정하고 나면 pivot보다 크고 오른쪽에 있는 숫자만 원래의 배열에 붙일 수 있다.
따라서 pivot의 뒤에 붙일 수 있는 부분수열을 만들고 만든 부분수열로 다시 LIS를 만들어서 원래의 수열S에 붙인다.
알고리즘 순서
간단한 분할 정복과 백트래킹 두 가지 방법으로 구현하였다.
[첫 번째 방법: 분할 정복]
먼저 가장 쉽게 구할 수 있는 분할 정복 알고리즘이다. 알고리즘의 순서는 다음과 같다.
- 현재 원소를 넣고 탐색하는 경우와 넣지 않고 탐색하는 경우를 모두 고려한다.
- 재귀 함수로 전의 과정을 반복한다.
- 기저 사례는 모두 탐색했을 때이다.
하지만 이 방법은 모든 경우를 다 탐색하므로 훨씬 비효율적이다. 따라서 탐색의 경로를 조금 더 줄일 수 있다.
다음은 백트래킹을 이용하여 조금 가지치기한 방법이다.
[두 번째 방법: 백트래킹]
- 하나의 원소를 pivot으로 정하고 pivot의 오른쪽에 있는 원소들 중 pivot보다 큰 원소로만 이루어진 부분 수열(A)을 만든다.
- 앞에서 만든 부분수열을 재귀 함수로 전달하여 앞의 과정을 반복하고 LIS를 구하고 가장 큰 LIS를 원래 수열에 붙인다.
- 백트래킹을 이용하여 pivot을 순차적으로 증가시키며 조합의 경로를 탐색한다.
- LIS의 길이가 커질 때마다 갱신한다.
완전 탐색으로 LIS를 구하는 알고리즘에서는 backtracking을 이용한 1~2의 과정이 이 알고리즘의 핵심이다.
다음은 이 알고리즘을 적용했을 때 돌아가는 예시이다. 글이 길어지므로 접은글로 작성하였다.
(보고 싶은 사람은 클릭)
예를 들어 S(1)을 pivot으로 설정하고 탐색한 경우를 살펴 보자.
S(n) = {10, {20, 10, 30, 20, 50} }
S(1)보다 크고 오른쪽에 있는 수들을 탐색하여 뒤에 붙일 수 있는 최대의 증가하는 부분 수열을 구한다.
이때 부분 수열을 만들 때 가장 중요한 두 조건은 두 가지이다.
- pivot보다 오른쪽에 있어야 한다.
- pivot보다 커야 한다.
따라서 j 는 i + 1 부터 n - 1까지 탐색한다.
위의 S(1)의 호출은 기본 호출이고 다음 호출부터가 재귀 호출이다.
다음은 기본 호출 이후 백트래킹을 이용해 조합의 경로를 재귀 호출로 탐색하는 과정이다.
중첩된 괄호의 수만큼 함수가 호출된다.
[첫 번째 재귀 호출 결과]
S(n) = {10, {20, 10, 30, 20, 50} }
j = 3, 5
pivot은 20이고 pivot의 오른쪽에 있는 수 중 pivot보다 큰 수만으로 이루어진 부분수열 A를 만든다.
만들어진 부분 수열은 {30, 50}이다.
[두 번째 재귀 호출 결과]
S(n) = {10, {20, {10, 30, 20, 50} } }
j = 3, 4, 5
pivot은 10이고 pivot의 오른쪽에 있는 수 중 pivot보다 큰 수만으로 이루어진 부분수열 A를 만든다.
만들어진 부분 수열은 {30, 20, 50}이다.
[세 번째 재귀 호출 결과]
S(n) = {10, {20, {10, {30, 20, 50} } } }
j = 5
pivot은 30이고 pivot의 오른쪽에 있는 수 중 pivot보다 큰 수만으로 이루어진 부분수열 A를 만든다.
만들어진 부분 수열은 {50}이다.
. . .
(같은 방법으로 다섯 번째 호출까지 호출된다)
. . .
[다섯 번째 재귀 호출 결과]
S(n) = {10, {20, {10, {30, {20, {50} } } } }
pivot은 50이고 pivot의 오른쪽에 있는 수 중 pivot보다 큰 수만으로 이루어진 부분수열 A를 만든다.
그런데 만들 수 있는 부분수열은 존재하지 않는다. 이는 코드로 구현할 때 base condition으로 이용한다.
이후 다섯 번째 호출을 종료하고 네 번째 호출로 돌아간다.
. . .
이렇게 백트래킹으로 재귀 호출을 반복하면서 마지막까지 탐색을 끝내고 나면 스택의 구조에 따라 역순으로 전의 호출로 돌아온다!
. . .
세 번째 호출로 돌아온 경우를 보자.
[세 번째 호출]에서 얻어진 LIS는 다음과 같이 두 가지이다.
30 + {50} : pivot이 30일 때 {50}이 붙은 값
20 + {50} : pivot이 20일 때 {50}이 붙은 값
50 + { } : pivot이 50일 때 아무 것도 붙지 않은 값
세 번째 호출의 LIS의 길이는 2로 같으므로 2를 반환한다. 이후 세 번째 호출을 종료하고 두 번째 호출로 돌아간다.
[두 번째 호출]에서 구해지는 LIS는 다음과 같다.
10 + {30, 50} : pivot이 10일 때 {30, 50}이 붙은 값
30 + {50} : pivot이 20일 때 {50}이 붙은 값
20 + {50} : pivot이 20일 때 {50}이 붙은 값
50 + { } : pivot이 50일 때 아무 것도 붙지 않은 값
두 번째 호출의 LIS의 길이는 3이 최대이므로 3을 반환한다. 이후 두 번째 호출을 종료하고 첫 번째 호출로 돌아간다.
[첫 번째 호출]에서 구해지는 LIS는 다음과 같다.
20 + {30, 50} : pivot이 20일 때 {30, 50}이 붙은 값
10 + {30, 50} : pivot이 10일 때 {30, 50}이 붙은 값
10 + {20, 50} : pivot이 10일 때 {20, 50}이 붙은 값
30 + {50} : pivot이 30일 때 {50}이 붙은 값
20 + {50} pivot이 20일 때 {50}이 붙은 값
50 : pivot이 50일 때 아무 것도 붙지 않은 값
첫 번째 호출의 LIS의 길이는 3이 최대이므로 3을 반환한다.
위의 예시를 보면 첫 pivot을 S(1)로 설정했기 때문에 S(1)에서 시작했을 때 얻을 수 있는 최대 LIS의 길이를 구한 것이다.
따라서 첫 pivot을 S(0)으로 설정하면 S(0)에서 시작했을 때 LIS의 최대 길이를 얻게된다.
알고리즘 구현
이를 알고리즘으로 구현한 코드이다.
위의 예시에서 볼 수 있듯이 더 이상 붙일 부분수열이 없거나 마지막까지 탐색한 경우가 기저사례이다.
[첫 번째 코드]
첫 번째 코드는 간단한 완전 탐색으로 구현하였다. 모든 원소들이 양수라고 가정하고 시작값을 -1로 하였다.
#include <iostream>
using namespace std;
int N;
int S[1000];
int LIS(int cur, int last){
if(cur == N) return 0;
if(S[cur] <= last) return LIS(cur+1, last);
return max(LIS(cur+1, last), 1 + LIS(cur+1, S[cur]));
}
int main()
{
cin >> N;
for(int i=0; i<N; i++) cin >> S[i];
cout << LIS(0, -1);
return 0;
}
[두 번째 코드]
두 번째 코드는 백트래킹으로 구현하여 불필요한 탐색을 조금이나마 줄였다.
//완전 탐색
#include<iostream>
#include<vector>
using namespace std;
vector<int> S;
int N;
//i번째에 대해 i+1 ~ N-1까지 순회하며 각각의 LIS를 반환하는 함수:
int LIS(const vector<int>& A) {
//base condition
if (A.empty()) return 0;
int ret = 0;
for (int i = 0; i < A.size(); i++) {
vector<int> B;
for (int j = i + 1; j < A.size(); j++) {
if (A[j] > A[i]) B.push_back(A[j]);
}
ret = max(ret, 1 + LIS(B));
}
return ret;
}
int main(void) {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
int num;
cin >> num;
S.push_back(num);
}
cout << LIS(S);
return 0;
}
완전 탐색 알고리즘 분석
위의 알고리즘을 적용하면 각각의 pivot마다 얻을 수 있는 수열은 두 가지이다.
- 자기 자신의 수열(더 이상 붙일 부분 수열이 존재하지 않는 경우)
- 자기 자신의 수열에 다음의 호출에서 구해진 LIS가 붙은 경우
이제 완전 탐색 알고리즘의 시간복잡도를 분석해보자.
첫 번째 코드는 넣는 경우와 안넣는 경우로 분기가 나누어지므로 시간 복잡도는 O(2ⁿ)이 자명하다.
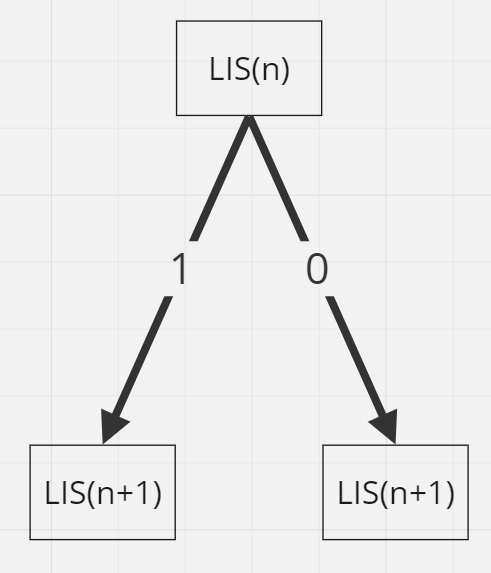
하지만 두 번째 코드는 반복문과 재귀의형태가 중첩되어 있어 얼핏 보면 O(N³)처럼 생각할 수 있다.
최악의 경우를 가정해 보자.
N이 너무 커지면 공간이 부족해지므로 N = 3이라고 하고 S = {1, 2, 3}이라고 가정하자.
LIS()함수를 주어진 배열을 탐색하며 만들 수 있는 증가하는 부분 수열의 최댓값을 반환하는 함수라고 정의하였다.
상태 공간 트리로 나타내 보면 아래의 그림처럼 두 번째 코드의 수행 과정을 보면 백트래킹을 이용한 탐색 과정에서도 두 개의 분기로 나누어진다.
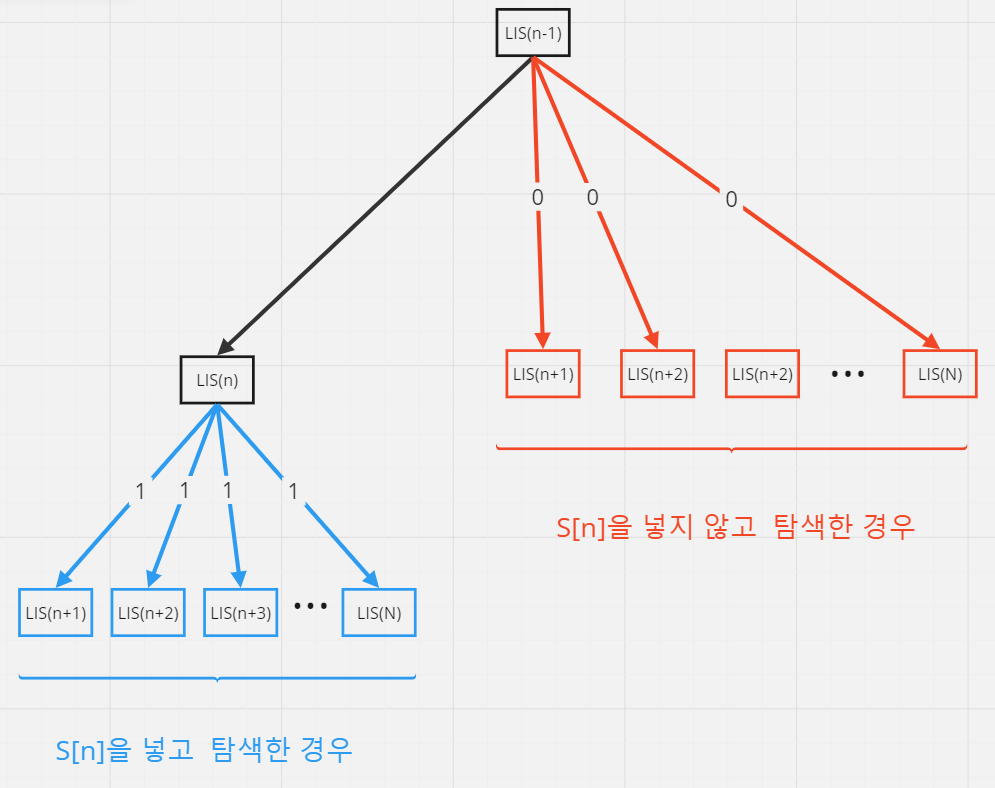
이를 LIS(0)부터 LIS(N)까지 일반화하면 다음의 구조가 된다.


이로부터 얻은 결과는 다음과 같다.
즉 반복문을 순회하며 반복 횟수(n)만큼 지수적(2ⁿ)으로 반복되는 것이다.
따라서 백트래킹을 이용한 탐색에서도 현재 값을 넣고 탐색하는 경우와 넣지 않고 탐색하는 경우로나누어지는 것을 알 수 있다.
따라서 두 번째 코드의 시간복잡도는 O(N³)이 아니라 O(2ⁿ)이 된다.
위의 결과에서 알 수 있듯이 완전 탐색 알고리즘은 어떤 방법을 쓰던지 상관없이 각각의 호출마다 무조건 두 개의 분기점이 생긴다.
따라서 일반적인 분할 정복을 이용하던 백트래킹을 이용하던 완전 탐색 알고리즘은 무조건 시간복잡도가 O(2ⁿ)이 된다.
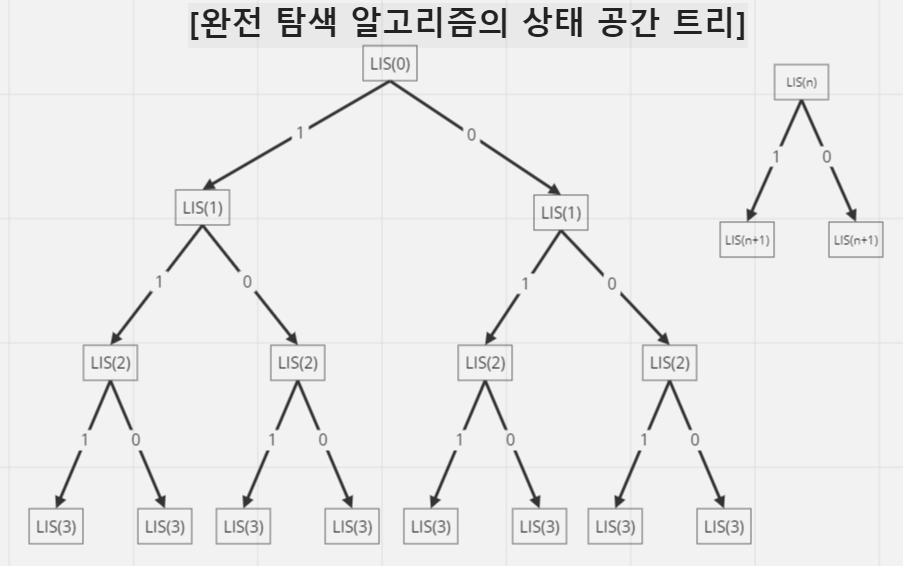
두 코드의 총 실행 과정을 상태 공간 트리로 나타내서 비교하면 다음과 같다.


분할 정복을 쓰던지 백트래킹을 쓰던지 상관없이 모두 2³인 8가지 탐색 경로가 있다는 것을 알 수 있다.
2) 동적 계획법을 이용한 LIS 알고리즘
아이디어
동적 계획법의 아이디어는 항상 완전 탐색으로부터 두 가지 특징을 발견하는 것으로 시작한다.
전의 완전 탐색 알고리즘으로부터 동적 계획법의 아이디어를 도출해 보자.

(1) Optimal Substructer(최적 부분 구조)
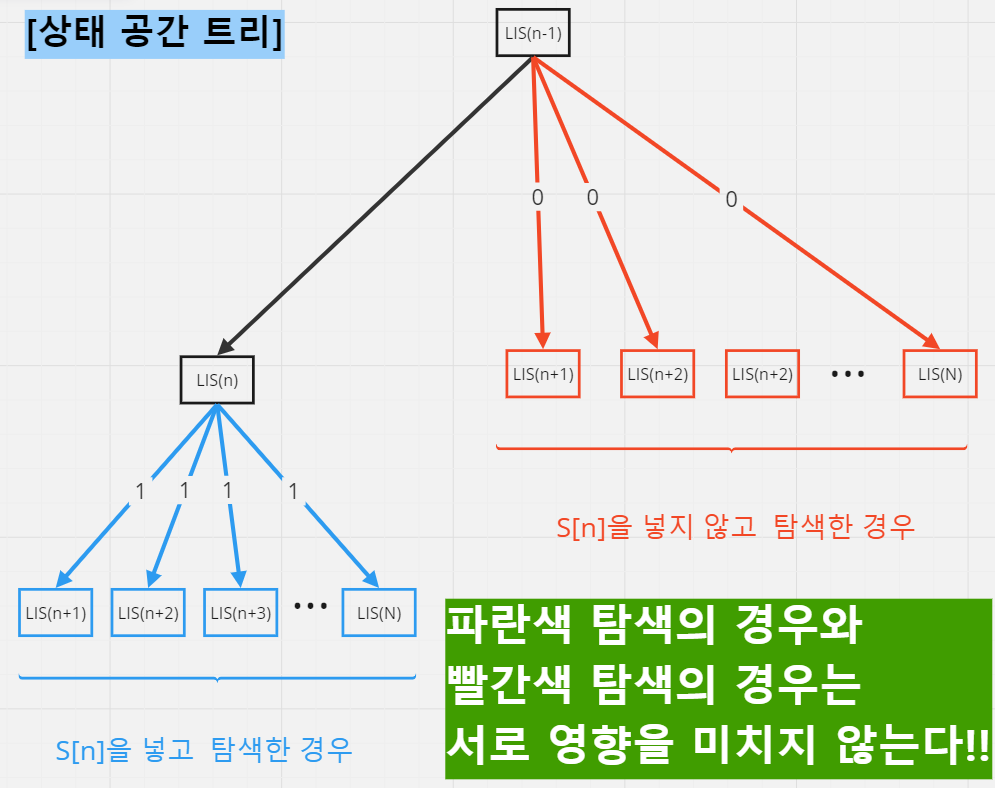
상태 공간 트리를 보면,
현재 원소 S(n)을 넣고 탐색하는 경우에서는 이 전의 입력이나 다음의 입력이 무엇인지 알 필요가 전혀 없다.
현재의 재귀 호출은 다른 재귀의 부분 문제들에 영향을 주지 않기 때문이다.
즉 각각의 부분 문제들이 독립적이다.
따라서 Optimal Substructer이 보장되는 것을 알 수 있다.
(2) Overlapping Subproblem(반복되는 부분 문제들)
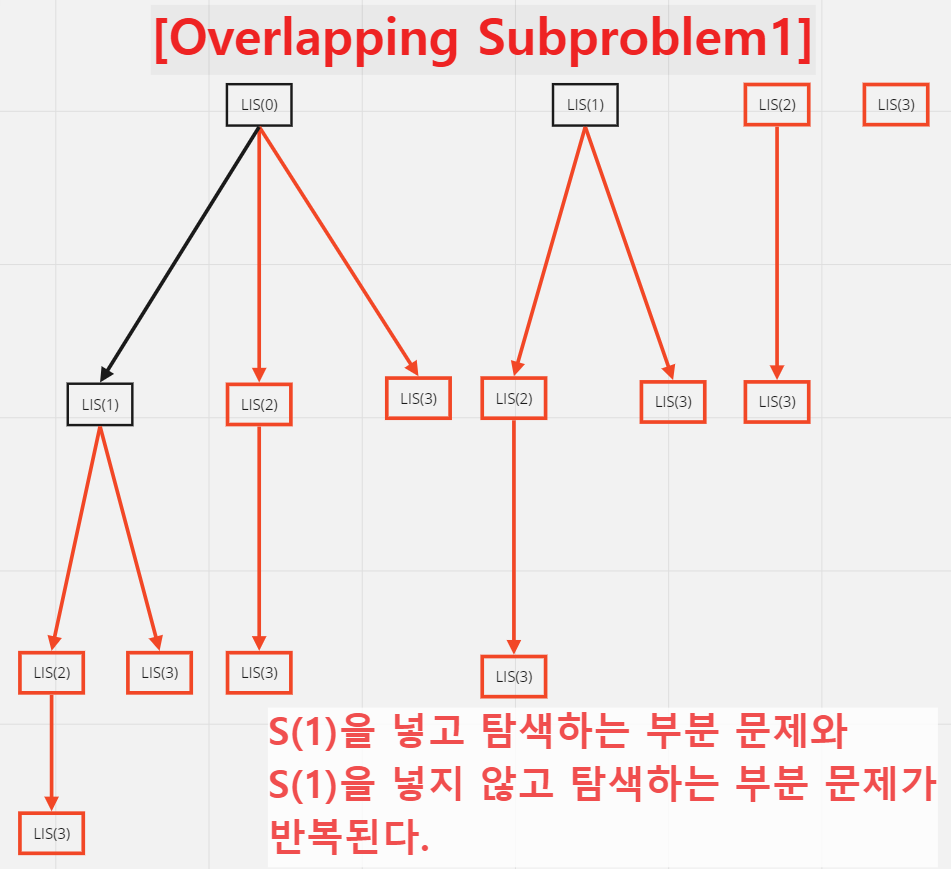
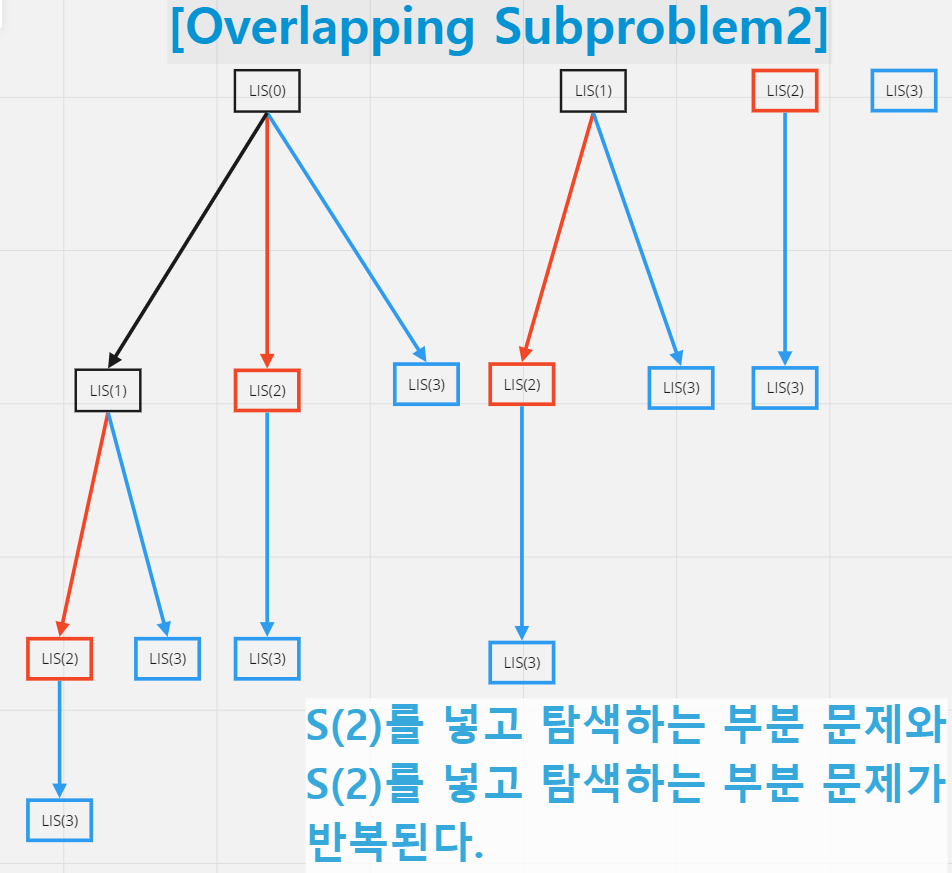
위의 탐색 구조를 보면 ,
S(1)을 넣고 탐색하는 부분 문제 1과 S(1)을 넣지 않고 탐색하는 부분 문제 1이 반복된다.
이후 나누어지는 각각의 탐색에 대해서도 ,
S(2)을 넣고 탐색하는 부분 문제 2와 S(2)을 넣지 않고 탐색하는 부분 문제 2가 반복된다.
이를 일반화하면 아래 그림과 같다.

For Loop를 순회하면서 다음이 부분 문제들이 2배씩 확장된다. 따라서 n번째 부분 문제는 2ⁿ번 반복된다.
실제로 위의 완전 탐색 알고리즘의 수행과정에서도,
두 번째 재귀 호출의 부분 문제가 세 번째 재귀 호출의 부분 문제와 겹치는 것을 알 수 있다.
자세한 예시는 접은글로 작성하였다. (궁금한 사람은 클릭)
세 번째 호출에서 LIS를 구하는 부분 문제
30 + {50} : pivot이 30일 때 {50}이 붙은 값
20 + {50} : pivot이 20일 때 {50}이 붙은 값
50 + { } : pivot이 50일 때 아무 것도 붙지 않은 값
세 번째 호출의 LIS의 길이는 2로 같으므로 2를 반환한다. 이후 세 번째 호출을 종료하고 두 번째 호출로 돌아간다.
두 번째 호출에서 LIS를 구하는 부분 문제
10 + {30, 50} : pivot이 10일 때 {30, 50}이 붙은 값
30 + {50} : pivot이 20일 때 {50}이 붙은 값
20 + {50} : pivot이 20일 때 {50}이 붙은 값
50 + { } : pivot이 50일 때 아무 것도 붙지 않은 값
두 번째 호출에서 순차탐색하며 pivot에 LIS를 붙이는 부분 문제는
세 번째 호출에서 pivot을 증가시키며 LIS를 붙이는 부분 문제와 겹친다.
즉, pivot을 바탕으로 넣는 경우와 넣지 않는 경우의 분기점이 생기는데 분기점마다 반복되는 부분 문제들이 기하급수적으로 생긴다.
이를 일반화해서 상태 공간 트리로 나타내면 다음과 같다.
따라서 각각의 하위 부분 문제들이 반복되는 것을 알 수 있다.
여기서 반복되는 부분 문제들의 특징을 보자.
재귀 함수는 LIFO(Last In First Out)의 구조를 가지므로 모든 탐색을 끝내고 호출이 종료되어 돌아올 때마다 다음의 특징을 가진다.
현재의 재귀 호출에서의 과정은 호출을 종료하고 이전 호출로 돌아가서 더 큰 문제에 포함되어 반복된다.
이 부분을 memoization하면 동적 계획법을 적용할 수 있다.
알고리즘 순서
- 부분 문제의 결과를 저장할 DP배열을 정의하고 원소의 값을 의미 없는 갑으로 초기화한다.
- 부분 문제의 해결 과정에서 memoization한 값이 있으면 그 값을 반한하고 memoization한 값이 없으면 새로 탐색하여 구한다.
- 현재 원소로 시작했을 때 구할 수 있는 LIS의 최대 길이를 구한다.
- 주어진 수열 S에 대해 모든 원소들의 LIS를 구하고 최댓값을 얻는다.
memozation을 적용하여 LIS() 함수를 정의하는 것이 핵심이다.
알고리즘 구현
두 가지 방법으로 구현하였다.
첫 번째 코드는 시작 값을 고정하여 top - down 방식으로 memoization하였고,
두 번째 코드는 마지막 값을 고정하여bottom - up 방식으로 memozation하였다.
[첫 번째 코드]
이 코드에서는 D(n)을 "S[n]으로 시작했을 때 얻을 수 있는 LIS의 최대 길이"라고 정의하였다.
#include<iostream>
#include<cstring>
using namespace std;
int N, ans;
int arr[1000];
int D[10000];
int LIS(int start) {
int& ret = D[start];
if (ret != -1) return ret;
ret = 1;
for (int i = start + 1; i < N; i++) {
if (arr[i] > arr[start]) ret = max(ret, 1 + LIS(i));
}
return ret;
}
int main(void) {
cin >> N;
memset(D, -1, sizeof(D));
for (int i = 0; i < N; i++) cin >> arr[i];
for (int i = 0; i < N; i++) ans = max(ans, LIS(i));
cout << ans;
return 0;
}
[두 번째 코드]
이 코드에서는 D(n)을 "S[n]으로 끝났을 때 얻을 수 있는 LIS의 최대 길이"라고 정의하였다.
코드..? 채울예정
알고리즘 분석
S = {1, 2, 3}인 경우 재귀를 이용한 Top - Down 방식과 반복문을 이용한 Bottom - Up방식 두 가지를 살펴보자.
[Top - Down방식]

Top - Down방식의 시간 복잡도를 살펴보자.
처음의 탐색의 경우마다 N의 깊이까지 재귀를 호출하며 memoization한다. → N+1번 탐색
main()함수에서 반복문을 순회하며 0부터 N까지 memoization한 값을 이용하여 비교한다. → N번 탐색
따라서 Top -Down방식의 시간복잡도는 O(N²)이다.
[Bottom - Up방식]
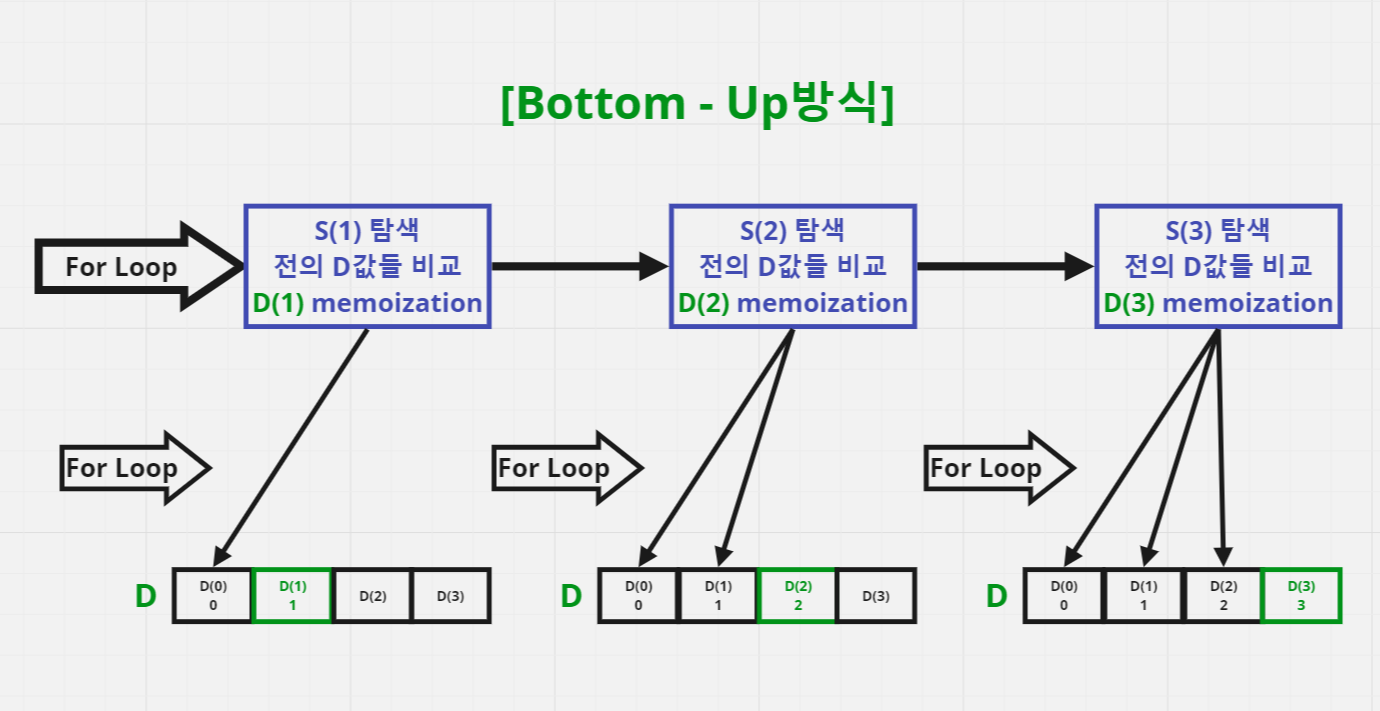
다음으로 반복문을 이용한 Bottom - Up 방식을 살펴 보자.
반복문을 순회할 때마다 N의 깊이까지 재귀를 호출하며 memoization한다. → N+1번 탐색
main()함수에서 반복문을 순회하며 0부터 N까지 memoization한 값을 이용하여 비교한다. → N번 탐색
따라서 Top -Down방식의 시간복잡도는 O(N²)이다.
알고리즘 최적화
첫 번째 코드는 top - down 방식으로 memoization했다.
그러므로 이미 LIS(0)을 실행하고 나면 순차적 재귀 호출에 의해 사실상 배열 D(n)에는 S(n)으로 시작했을 때 얻을 수 있는 LIS의 최대 길이가 채워져 있다.
함수를 호출하는 것도 메모리와 시간이 걸리므로 main() 함수에서 순차탐색마다 LIS() 함수를 호출하는 대신 D[i]를 가져오면 최적화할 수 있다.
3) 이분 탐색을 이용한 LIS 알고리즘
4) 세그먼트 트리를 이용한 LIS 알고리즘
https://nicotina04.tistory.com/167
최장 증가 부분 수열 LIS(Longest Incresing Sequence)
본론에 들어가기 앞서 작성자는 기존의 LIS를 구하는 법을 알려주던 블로그에서 알려주지 않았던 내용에 대해 한 번 데고 분노하여 직접 LIS에 대해 다루기로 했다. 평소였으면 이런 글에는 사족
nicotina04.tistory.com
https://loosie.tistory.com/376
[알고리즘] 가장 긴 증가하는 부분 수열 LIS - DP & 이진탐색 (Java)
가장 긴 증가하는 부분 수열 LIS LIS(Longest Increasing Subsequence)는 불연속 상관없이 가장 긴 증가하는 부분 수열을 구하는 알고리즘이다. 예시로, 수열 A = {10, 20, 10, 30, 20, 50}이 있다고 하면 해당 수열
loosie.tistory.com
최장 증가 부분 수열 ( LIS )
Table of Contents 개요 O(n^2) 풀이 더 알아보기 : O(n log n) 풀이 1 더 알아보기 : O(n log n) 풀이 2 1. 개요 최장 증가 부분 수열 (longest increasing subsequence) 문제는 유명한 동적 계획법 활용 예시입니다. LIS 문
www.weeklyps.com
DP: O(N제곱)
세그먼트 트리: O(N log N)
두 가지 예제 모두 풀어보자. 매우중요한 알고리즘 유형 중 하나이ㅏㄷ.
+ 전깃줄 문제 등을 통해
'자료구조 | 알고리즘 > 동적 계획법' 카테고리의 다른 글
| [알고리즘] 위상정렬 DP (0) | 2024.04.30 |
|---|---|
| [알고리즘] (수학, 동적 계획법) N/M수 분할 알고리즘 (자연수 분할) (0) | 2023.11.30 |
| [알고리즘] 최장 증가하는 부분 수열 알고리즘(완전 탐색, DP, 이분 탐색, 세그먼트 트리) (0) | 2023.11.29 |
| [알고리즘] 최대 연속 부분수열 합(Miximum subarray) 구하기 (0) | 2023.11.24 |
| [알고리즘] 동적 계획법을 이용하여 구간합 구하기(Prefix Sum) (0) | 2023.10.31 |

경이로운 BE 개발자가 되기 위한 프로그래밍 공부 기록장
도움이 되었다면 "❤️" 또는 "👍🏻" 해주세요! 문의는 아래 이메일로 보내주세요.
![[알고리즘] 최장 증가하는 부분 수열 알고리즘(완전 탐색, DP, 이분 탐색, 세그먼트 트리)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FlOqAu%2FbtsA7Nq2yoj%2FAAAAAAAAAAAAAAAAAAAAAKH9zGg1uLWYq-LMyD8JK1mvYiyUmPbwUGaDQI2KdnTt%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3DA1Igz8rj2z98STKCsLEjlBXPeOc%253D)