![[알고리즘] 유니온 파인드(Union Find)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbvNHXm%2FbtsGh3VZnxe%2FAAAAAAAAAAAAAAAAAAAAAO4AAn1op8YTrkp6p1b9MzdVdGZ5EWQm8iLwX_LatTCV%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3DePj2Iy1nZC89PHDztpXWjm0qm4Y%253D)

이번 포스팅에서는 유니온 파인드 알고리즘에 대해서 알아보겠습니다. 유니온 파인드를 알기 위해 간단한 트리의 개념을 알아야 합니다. 트리가 처음이라면 먼저 간단하게라도 트리의 개념과 트리 순회를 알아보고 오는 것을 추천드립니다.
유니온 파인드 알고리즘은 기본 구현보다 최적화 방법과 문제 적용이 더 중요합니다. 최적화 원리까지 이해하고 문제 적용하는 것을 강력 권장합니다.
1. 유니온 파인드란?
다음과 같이 여러 노드간의 연결 관계가 주어졌다고 해봅시다.
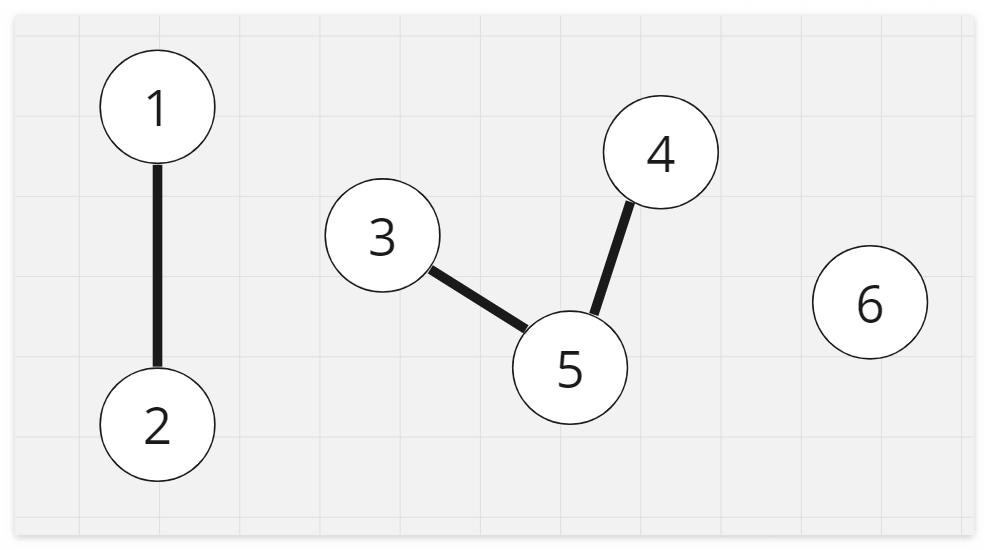
임의의 두 노드가 주어졌을 때 유니온 파인드 알고리즘을 이용하면 두 노드가 같은 집합에 속하는지 확인할 수 있습니다.
예를 들어 1과 2는 같은 집합, 3과 5도 같은 집합, 4와 6은 다른집합입니다. 유니온 파인드를 이용하면 이러한 연산을 O(1)에 바로 알 수 있습니다. 만약 M개의 쿼리가 주어졌다면 총 연산의 시간복잡도는 O(M*𝛼(N))이 됩니다. 여기서 𝛼(N)은 매우 느리게 증가하는 함수로 일반적인 상황에서 4에 수렴하므로 상수와 같습니다.
그러므로 유니온 파인드를 이용하면 분리 집합 여부를 상수의 시간복잡도로 알아낼 수 있습니다. (궁금하시면 애커먼 함수에 대한 증명을 찾아보세요)
[참고] 애커먼 함수에 대한 시간복잡도
𝛼(𝑁)은 애커먼(Ackermann) 역함수로 매우 빠르게 증가하는 애커먼 함수로부터 정의됩니다.
- 1 ≤ N < 3인 경우, α(N) = 1
- 3 ≤ N < 7인 경우, α(N) = 2
- 7 ≤ N < 63인 경우, α(N) = 3
- 63 ≤ N < 2⁶⁵⁵³⁶인 경우, 𝛼(N) = 4
- N ≥ 2⁶⁵⁵³⁶인 경우, 𝛼(N) = 5
𝛼(N)의 4번째 조건부터는 N의 상한은 무한에 가깝기 때문에 일반적으로 𝛼(N) = 4로 볼 수 있습니다. 따라서 Union-Find 알고리즘은 상수 시간복잡도로 분리집합 여부를 판단할 수 있습니다.
유니온 파인드는 다음과 같은 특징이 있습니다.
특징
- 서로소 집합, 상호 베타적 집합(Disjoint-Set) 혹은 분리 집합이라고도 한다.
- 집합 여부는 트리 구조로 나타낸다.
- 연결 관계를 만들어주는 Union 연산과 합집합 여부를 판단해주는 Find연산으로 이루어져 있다.
- 경로 최적화와 랭크 최적화로 최적화할 수 있다.
위에서 분리 집합이라는 말은 교집합이 없는 둘 이상의 집합을 저장하는 자료 구조를 의미합니다.
2. 알고리즘 구현
1) 알고리즘 순서
유니온 파인드 알고리즘은 크게 Union과 Find 두 가지 연산으로 구성됩니다. 알고리즘 순서는 다음과 같습니다.
- 부모의 정보를 초기화합니다.
- Union 연산으로 두 노드를 결합합니다.
- Find 연산으로 노드의 루트 노드를 찾습니다.
위의 과정이 끝나면 IsUnion 연산으로 두 노드가 같은 집합인지 아닌지 판별할 수 있습니다.
2) 구현
부모 정보 초기화
int par[1000001];
for(int i=1; i<=N; i++) par[i] = i;배열의 인덱싱을 이용하여 부모의 정보를 기록합니다. 배열의 원소는 각 노드의 부모 노드를 의미합니다. 부모 노드가 자기 자신이면 현재 노드가 루트노드(최상단 노드)입니다. 만약 다른 값을 가지면 그 값이 부모임을 의미합니다.
Find 함수
int Find(int x) {
return par[x] == x ? x : Find(par[x]);
}Find 함수는 x의 최상단 노드를 찾아주는 함수입니다. x가 최상단 노드이면 현재 노드를 반환합니다. 만약 x의 부모가 존재하면 재귀적으로 최상단 노드를 찾아서 반환합니다.
Union 함수
void Union(int x, int y) {
x = Find(x);
y = Find(y);
if (x < y) par[y] = x;
else par[x] = y;
}Union 함수는 두 노드를 연결짓는 함수입니다. 이때 관례적으로 더 작은 루트 노드를 부모 노드로 연결하면 편합니다.
IsUnion 함수
bool IsUnion(int x, int y) {
return Find(x) == Find(y) ? true : false;
}IsUnion 함수는 두 노드의 루트 노드가 같은지만 판별합니다. 같으면 true, 다르면 false를 반환합니다.
3) 최적화
위의 코드로 Union 연산과 Find 연산을 해보면 특정 입력에서 트리의 편향 일어나서 깊이가 커질 수 있습니다. 트리의 깊이는 탐색 시간을 결정하는 중요한 요소이므로 최적화를 통해 강제로 균형잡힌 트리를 유지해야 합니다.
최적화의 종류에는 크게 경로 최적화와 랭크 최적화가 있습니다.
경로 최적화(Path Compression)
아래의 Union 연산들을 수행해 보겠습니다. 다음은 트리의 편향이 일어나는 입력 예시입니다.
Union(2, 3) → Union(4, 5) → Union(5, 6) → Union(6, 7) → Union(8, 9) → Union(9, 10)
위의 예시처럼 트리의 편향이 일어난다면 최악의 경우 트리의 깊이가 N이 되어 Find함수의 시간 복잡도는 O(N)이 될 것이고 연산의 횟수가 M인 경우 전체 시간 복잡도는 O(NM)이 됩니다. 이러면 유니온 파인드를 쓰는 의미가 없어집니다. 따라서 트리의 편향 문제를 해결하기 위해 경로 최적화를 사용합니다.
모든 노드가 루트 노드를 가리킨다면 부모를 통해 하나씩 루트 노드를 찾을 필요가 없겠죠. 경로 최적화는 모든 노드가 루트 노드를 가리키도록 하는 최적화 방법입니다. 경로 최적화를 적용하면 트리의 구조는 왼쪽에서 오른쪽 형태로 바뀌게 됩니다.


이를 코드로 구현해 봅시다.
int Find(int x) {
return par[x] == x ? x : par[x] = Find(par[x]);
}경로 최적화는 Find함수에서 이루어집니다. 최초의 루트 노드를 찾을 때 부모를 루트 노드로 업데이트 시키기만 하면 다음 Find 연산때 루트 노드를 찾는 시간은 O(1)이 됩니다. 이는 경로 압축이라고도 합니다.
랭크 최적화(Union By Rank)와 사이즈 최적화(Union By Size)
경로 최적화를 했더라도 여러 집합들을 Union연산하는 과정에서 트리의 깊이가 깊어질 수 있습니다. 경로 압축의 예시에서 다음의 연산을 추가해 보겠습니다.
→ Union(4, 8) → Union(2, 4) → Union(8, 9) → Union(1, 2)
위의 Union 연산에서 더 작은 루트노드의 값을 부모 노드로 정했습니다. 위의 Union 연산들을 수행하면 트리의 깊이가 깊어집니다. 트리의 깊이를 작게 유지하기 위해 랭크 최적화를 적용합니다.
두 집합이 Union연산될 때 작은 루트노드값 대신 깊이가 큰 집합을 부모 노드로 정하면 트리의 깊이를 최소로 유지할 수 있습니다. 랭크 최적화를 적용하게 되면 트리의 구조는 왼쪽에서 오른쪽 형태로 바뀌게됩니다.


랭크 최적화를 하기 전 트리의 깊이는 4인 반면, 적용 후 트리의 깊이는 2가 되었습니다.
이를 코드로 구현해 보겠습니다. 랭크 최적화를 하기 위해서는 먼저 트리의 깊이를 배열에 저장하고 Union 연산시 어느 집합이 더 깊은지 비교해야 합니다.이때 배열에 트리의 깊이를 저장할 수도 있고 트리의 사이즈를 저장할 수도 있습니다. 트리의 깊이를 기준으로 비교하는 것을 랭크 최적화, 트리의 사이즈를 기준으로 비교하는 것을 사이즈 최적화라고 합니다.
[랭크 최적화(Union By Rank)]
void Union(int x, int y) {
int res = 0;
x = Find(x);
y = Find(y);
if (Rank[x] == Rank[y]) Rank[x]++;
if (Rank[x] > Rank[y]) par[y] = x;
else par[x] = y;
}랭크 최적화는 트리의 깊이를 Rank 배열로 저장하고 Union 연산시 두 루트노드의 깊이를 비교하여 더 깊은 깊이를 가진 루트 노드를 부모 노드로 정합니다. 이때 랭크 최적화를 이용하여 Union하는 방법에는 두 가지가 있습니다.
- 두 집합의 깊이가 같은 경우 → Union이후에 부모 노드의 깊이가 1 증가합니다.
- 두 집합의 깊이가 다른 경우 → 깊이가 더 깊은 루트 노드는 이미 작은 루트 노드보다 크므로 Union이후에 아무런 변화가 없습니다.
위의 두 가지만 잘 고려해서 Union만해주면 됩니다. 그런데 생각이 깊은 사람이라면 여기서 의문이 들 수 있습니다. 이후에 Find연산을 이용하여 경로압축을 할 경우 깊이가 바뀌게 되고 이를 갱신하는 기능은 따로 없습니다. 즉, 아래의 왼쪽 트리에서 Find(3), Find(9), Find(10)연산을 하고 나면 경로 오른쪽 트리처럼 구조가 바뀝니다.

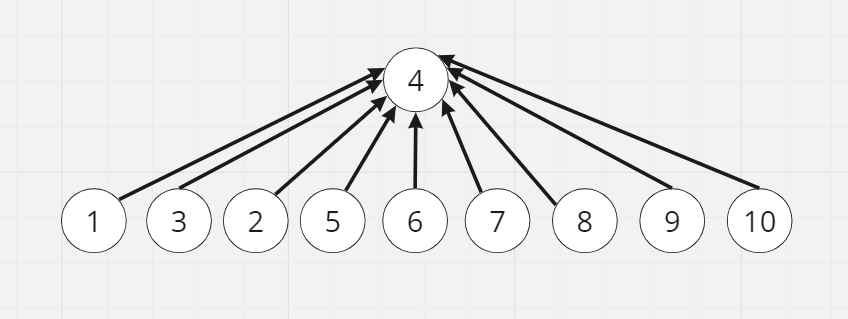
이렇게 되면 다음 Union연산시 깊이를 비교할 때 정확한 깊이로 비교할 수 없게 됩니다. 하지만 경로압축할 때마다 해당집합의 모든 노드를 검사하며 트리의 높이를 갱신하는 것은 오히려 연산의 시간이 증가하므로 비효율적입니다. 따라서 Find연산마다 깊이를 업데이트하지 않습니다. 그 대신 추상화된 트리의 깊이를 나타내는 랭크를 사용하여 표현합니다. Rank에 저장된 정보는 트리의 깊이를 정확히 나타내지는 않지만 깊이에 비례하는 값들입니다.
[사이즈 최적화(Union By Size)]
void Union(int x, int y) {
int res = 0;
x = Find(x);
y = Find(y);
if (siz[x] > siz[y]) par[y] = x, siz[x] += siz[y];
else par[x] = y, siz[y] += siz[x];
}사이즈 최적화는 트리의 크기를 siz배열로 저장하고 Union 연산시 사이즈가 큰 집합의 루트 노드를 부모 노드로 정합니다. 나머지는 랭크최적화와 같습니다.
Weighted Union-Find
위의 랭크 최적화와 사이즈 최적화를 구현하면 부모의 정보와 깊이 또는 크기를 저장해야 합니다. 배열을 두 개 사용하므로 메모리 사용량이 두 배가 됩니다. weighted-union-find를 사용하면 공간 복잡도또한 최적화할 수 있습니다.
weighted-union-find는 루트 노드에 집합의 깊이 or 사이즈를 음수로 저장합니다. 이렇게 하면 부모의 정보 배열 하나로 깊이 or 사이즈까지 표현할 수 있습니다.

위의 구조에서 par[4] = -4, par[6] = 4가, par[2] = -2 입니다. Union연산시 크기를 비교할 때에는 절댓값을 이용해 비교해주면 됩니다.
weighted union find를 사용하면 Find와 Union만 살짝 수정해주면 됩니다. 코드는 아래와 같습니다.
[Find 함수]
int Find(int x) {
return par[x] < 0 ? x : par[x] = Find(par[x]);
}par의 값이 음수일 경우 루트노드임을 의미합니다. 따라서 par값이 양수일 때에만 탐색하며 재귀적으로 경로 압축을 진행합니다.
[Union 함수]
void Union(int x, int y) {
x = Find(x);
y = Find(y);
if (par[x] == par[y]) par[x]--;
//Rank가 음수이므로 더 작은 수가 큰 랭크를 의미
if (par[x] < par[y]) par[y] = x;
else par[x] = y;
}루트 노드에는 Rank 정보가 음수로 저장되어 있으므로 더 작은 값이 실제로는 더 큰 Rank를 가집니다. 이를 고려하여 비교해주면 됩니다. 나머지는 앞의 Union By Rank와 동일합니다.
[백준 1717] 집합의 표현 문제를 풀어보면서 코드를 검증해 보세요. 간단한 유니온 파인드를 구현하는 문제입니다.
아래는 경로 최적화, 랭크 최적화, Weighted Union Find를 모두 적용하여 구현한 코드입니다.
#include<iostream>
#include<vector>
using namespace std;
vector<int> par(1000001, -1);
int N, M;
int Find(int x) {
return par[x] < 0 ? x : par[x] = Find(par[x]);
}
bool isUnion(int x, int y) {
return Find(x) == Find(y) ? true : false;
}
void Union(int x, int y) {
x = Find(x);
y = Find(y);
if (isUnion(x, y)) return;
if (par[x] == par[y]) par[x]--;
//Rank가 음수이므로 더 작은 수가 큰 랭크를 의미
if (par[x] < par[y]) par[y] = x;
else par[x] = y;
}
int main(void) {
cin.tie(0);
ios_base::sync_with_stdio(0);
cin >> N >> M;
while (M--) {
int order, a, b;
cin >> order >> a >> b;
if (!order) Union(a, b);
else {
if (isUnion(a, b)) cout << "YES\n";
else cout << "NO\n";
}
}
return 0;
}
첫 번째 코드가 세 가지 최적화를 모두 적용한 코드이고, 두 번째 코드가 랭크 최적화와 경로 압축만, 세 번째 코드가 경로 압축만 적용한 코드입니다. 확실히 랭크 최적화까지 적용한 코드가 시간적인 면에서 2배 이상 빠른 것을 알 수 있습니다. 또한 Weighted Union Find를 사용한 코드가 공간 복잡도도 조금이나마 줄어든 것을 볼 수 있습니다.
일반적인 경우에는 Find연산을 통한 경로 압축만 해도 시간복잡도를 크게 줄일 수 있습니다. 하지만 쿼리가 더 많아지거나 다른 알고리즘에 함께 사용해서 시간복잡도를 최대한 줄여야 하는 경우 경로압축과 랭크최적화까지 적용해야 하는 경우도 있습니다. 평소에 미리 익혀놓고 필요할 때 자유자제로 쓰는 것을 권장합니다.
3. 활용
유니온 파인드는 기본적으로 합집합찾기, 서로소 집합 판별 문제를 해결할 때 사용됩니다. 보통 유니온 파인드 한 개념만 쓰이기 보다는 다른 알고리즘에 활용되어 쓰이는 경우가 많습니다. 특히 여러 노드간의 분리 집합 여부를 판단하는 과정에서 브루트 포스와 함께 활용됩니다.
대표적인 예시로는 최소 공통 조상(Lowest Common Ancester), 최소 신장 트리(Minimum Spanning Tree) 알고리즘을 구현합니다. 따라서 유니온 파인드를 익히고 LCA, MST(크루스칼 알고리즘, 프림 알고리즘)까지 구현할 줄 알아야 합니다.
'자료구조 | 알고리즘 > 심화 알고리즘' 카테고리의 다른 글
| [알고리즘] 시물레이션(구현) (0) | 2024.04.09 |
|---|---|
| [알고리즘] 트리DP (0) | 2024.01.12 |
| [알고리즘] 최소 스패닝 트리(MST) (0) | 2024.01.12 |
| [알고리즘] 최단 경로 알고리즘에 대한 아이디어 (0) | 2023.12.31 |
| 애드 훅 (0) | 2023.12.30 |

경이로운 BE 개발자가 되기 위한 프로그래밍 공부 기록장
도움이 되었다면 "❤️" 또는 "👍🏻" 해주세요! 문의는 아래 이메일로 보내주세요.
![[알고리즘] 시물레이션(구현)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FdoHccK%2FbtsGtUZR3Du%2FAAAAAAAAAAAAAAAAAAAAAO_Wqg2en3r-2e7u-AYXNLzVmkgDzP4_htyBc--9OxCN%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3DkdDnKMCZHqEF2%252BZLia%252FJhu5umXU%253D)
![[알고리즘] 트리DP](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fdg2p1z%2FbtsGDJ4vCD2%2FAAAAAAAAAAAAAAAAAAAAANxeAN0b9oKX6T9jDULPEoyryIQo08CoGKwPIyNeoEjd%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3D9evZvUQOOiuxBZenrShPmHyynzk%253D)
![[알고리즘] 최소 스패닝 트리(MST)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FuqIyI%2FbtsGtlW5TSR%2FAAAAAAAAAAAAAAAAAAAAAHNmW1TJh09nbaFbo8a7ZUbEJlWqMAPT7Yqrha4dqlYO%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3DjJS56Nl6CHoXCR6GhmDgboSdjFA%253D)