[알고리즘] 탐욕법(Greedy)

이번 글에서는 그리디 알고리즘에 대해 다루어 보겠습니다. 가장 대표적인 예제인 동전 문제와 회의실 배정 문제와 함께 다룰 예정이니 참고해 주세요

1. 탐욕법이란?

탐욕법이란 미래를 고려하지 않고 현재 가장 최선의 선택을 하는 알고리즘입니다. 쉽게 말하면 한 번 선택하고 난 후 앞이나 뒤를 전혀 돌아보지 않는 알고리즘입니다. 

 

2. 특징

그리디 알고리즘에서는 다음의 특징을 가집니다. 

• 그리디 선택 속성(Greedy Choice Property)
  현재 선택은 미래의 선택에 영향을 미치지 않습니다. 이를 그리디 선택 속성이라고 합니다.
• 최적 부분 구조
  현재 선택들이 모여 전체의 최적해를 보장해야만 믿고 현재 최선의 선택을 할 수 있습니다.
  
  

앞에서 말했듯이 미래의 선택을 고려하지 않고 과거도 돌아보지 않기 때문에 위의 두 조건만 성립한다면 완전 탐색보다 훨씬 빠른 속도로 해결할 수 있습니다.

따라서 위의 두 성질을 만족하는 지 확인하기 위해 노력하는 것이 문제 풀이이 핵심 포인트 입니다.

 

3. 그리디적 사고

문제를 읽고 어떻게 이 문제가 그리디라고 떠올릴 수 있을까요?

그리디 문제들은 보통 참신한 발상을 요구하거나 수학적 감각을 요구하는 경우가 많습니다. 흔히 "많이 풀어보며 그리디적 감을 익혀야 한다"라고 하지만 저는 그 말도 와닿지가 않았습니다. 그래서 저는 보통 저만의 원칙을 세워서 접근하는 편입니다. 모든 문제에 적용되는 것은 아니지만 저만의 사고과정을 정리해보면 다음과 같습니다.

그리디는 완전 탐색의 속도를 개선하기 위해 만들어진 알고리즘입니다. 이 원리를 바탕으로 우선 완전 탐색을 통해 시뮬레이션해보는 과정에서 완전 탐색으로 최적해를 떠올릴 수 없다면 그리디를 생각해볼 수 있습니다. 

일관된 접근 방식

1. 문제에서 데이터의 크기를 보고 완전 탐색의 방법을 떠올려본다.
2. 완전탐색으로 시간내에 해결할 수 없다면 DP 등 완전 탐색을 보완할 방법을 떠올려본다.
3. DP, 두 포인터 등으로도 시간내에 해결할 수 없다면 그리디를 생각해본다.
4. 그리디를 생각했다면 의심과 증명으로 가설을 검증해본다.

그리디적 발상은 갑자기 떠오르는 것이 아닙니다. 위와 같은 사고과정 속에서 충분히 의심해볼 수 있는 상황일 때 한 번 의심해보는 것에서 시작하는 경우가 대부분입니다. 따라서 일관된 문제 풀이 습관이 중요합니다.

위 과정에서 의심과 증명에 대해서 자세히 살펴보겠습니다.

의심

한번 그리디를 떠올렸다면 간단한 조작을 통해서 부분 최적해가 전체 최적해를 만족할 수 있는지 의심해 봅니다. 이 조작 과정에서는 보통 정렬, 데이터 인덱싱 등이 있습니다. 쉽게 말하면 현재 최선의 선택만 해서 최적의 결과를 얻을 수 있도록 데이터를 예쁘게 다듬어 보는 것입니다. 이 과정에서 가장 중요한 것은 데이터의 정렬 기준입니다. 

이후 탐색할 때 미리 알고 있는 정보를 바탕으로 최선의 선택만 하면 됩니다.

증명

보통 내가 떠올린 발상이 적용가능한지 귀류법으로 간단하게 검증해보고 문제풀이에 들어갑니다. 검증을 위해서는 앞서 말한 그리디의 특징인 "그리디 선택 속성"과 "최적 부분 구조" 두 가지가 성립하는지 검증해봐야 합니다.

하지만 실전에서는 하나하나 검증할 시간이 없습니다. 따라서 실전에서는 그리디가 맞는 것 같은 경우 증명없이 바로 한 번 시도해보고 안되면 넘어가야 합니다. 돌아와서 다시 보면 그리디가 아닐 수도 있기 때문이죠.

그러므로 평소에 많은 문제들로 열심히 검증하려고 노력해보고, 실전에서는 그냥 써야 합니다.

 

4. 예제

예제1: [백준 11047] 동전 0

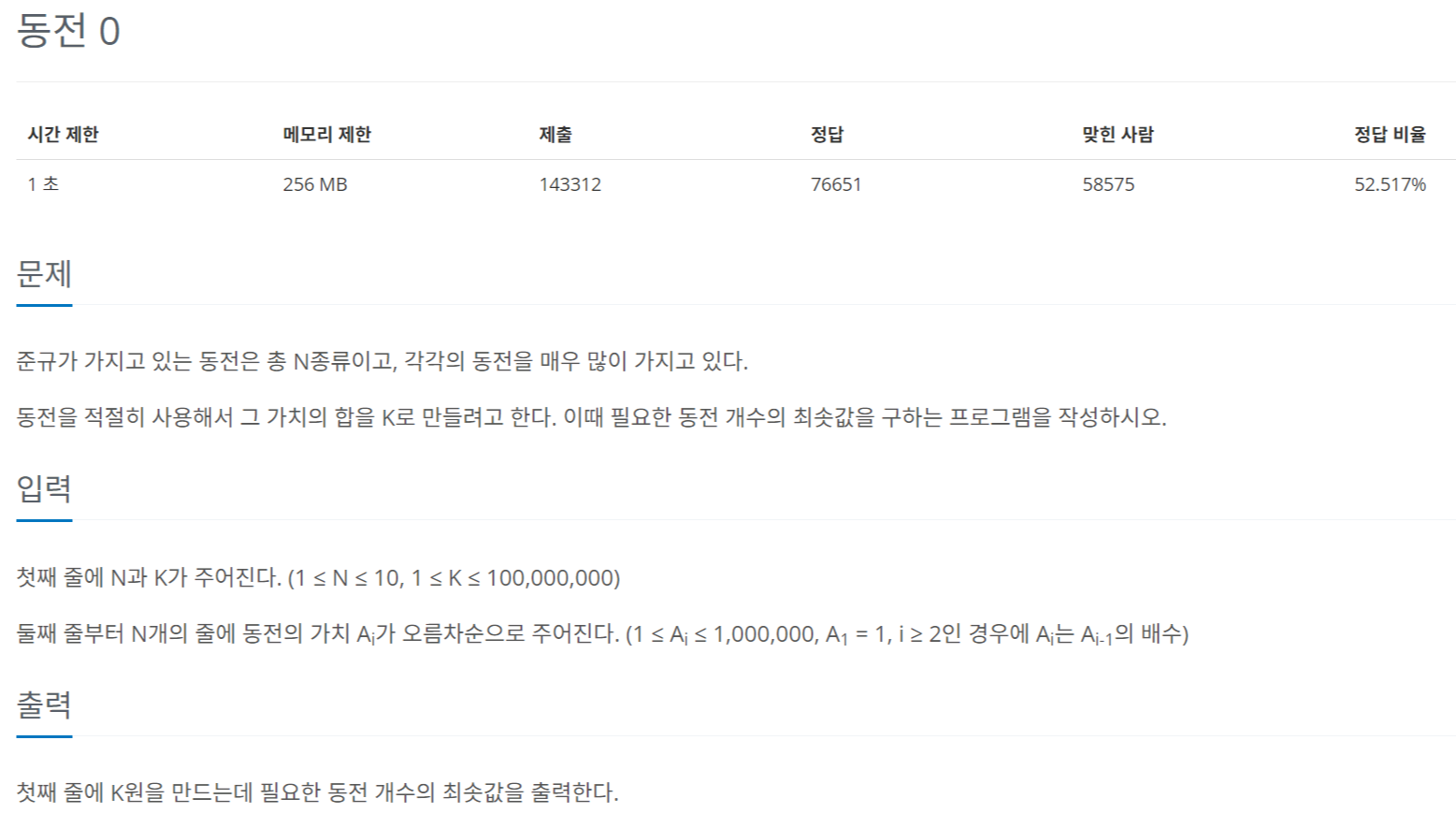
이 문제는 동전 문제라고도 불리는 유명한 그리디 예제 입니다. 이 문제를 통해서 그리디적 사고를 살펴보겠습니다.

1. 완전 탐색으로 시작해보기
   K = 1억입니다. 따라서 모든 동전으로 1억원을 조합해보는 가지수를 따져보면 1억번이 넘습니다. 완전 탐색으로는 무조건 1초 안에 해결이 불가능합니다.
2. DP로 생각해보기
   조합으로 2차원 배열을 통해 데이터를 설정할 수는 있습니다. 하지만 256MB의 메모리 제한이 있으므로 1억칸 짜리 배열을 선언하면 메모리 초과가 발생할 것입니다.
3. 그리디 떠올리고 의심해보기
   완전 탐색으로 최적해를 찾기 힘들 것 같아 그리디를 떠올려 볼 수 있습니다. 동전의 크기 순서대로 정렬한 후 큰 동전으로 먼저 바꾸면 최소 동전으로 바꿀 수 있을 것 같습니다.
4. 간단한 검증
   귀류법(크기순으로 하지 않았을 때 최소가 나올 수 있다고 가정하고 거짓임을 보인다)으로 확인한 후 문제풀이를 하면 됩니다. 이 방법은 그리디 선택 속성과 최적 부분 구조를 모두 만족합니다.

여기서 가장 중요한 데이터의 정렬 기준은 "동전의 크기"입니다.

정답 코드 보기

#include<iostream>

using namespace std;

int money[10];

int main(void) {
    ios::sync_with_stdio(0);
    cin.tie(0);
    int N, K;
    int idx = 0;
    int ans = 0;

    cin >> N >> K;
    for (idx = 0; idx < N; idx++) cin >> money[idx];

    for (int i = N - 1; i >= 0; i--) {
        ans += K / money[i];
        K %= money[i];

    }
    cout << ans;

    return 0;
}

 

예제2: [백준 1931] 회의실 배정

이 문제는 간격 스케줄링이라고도 불리는 유명한 그리디 예제 입니다. 이 문제도 일관된 사고를 적용해 보겠습니다.

1. 완전 탐색으로 시작해보기
   각 회의는 넣는 경우/넣지 않는 경우 두 가지를 가지므로 모든 조합의 수는 2ⁿ가지 입니다. N = 10만이므로 절대로 불가능합니다.
2. DP로 생각해보기
   DP로 memoization 또는 tablation해도 O(N²)입니다. N = 10만이므로 1초 안에 절대로 불가능합니다.
3. 그리디 떠올리고 의심해보기
   완전 탐색으로 최적해를 찾기 힘들 것 같아서 그리디를 떠올려 봅니다. 짧은 회의 시간 순서대로 정렬해보고 시뮬레이션해보니 반례가 존재합니다. 데이터의 정렬 조건을 찾다가 끝나는 시간이 빠른 순서대로 정렬하면 최소가 될 것 같습니다.
4. 간단한 검증
   반례가 존재하지 않고 데이터의 정렬 시간인 O(NlogN)의 시간으로 해결할 수 있습니다.

여기서 가장 중요한 데이터 정렬 기준은 "끝나는 시간"입니다.

정답 코드 보기

#include<iostream>
#include<algorithm>

using namespace std;

//2차원 배열을 사용해도 되고, start, end배열을 각각 사용해도 됨!
//2차원 배열: task[2][100000]
//start, end 따로 사용: st[100000], en[100000]
pair<int, int> task[100000];

int N, ans;

void solve() {
	//가상의 선을 당긴다고 생각하고 탐색
	int en = 0;
	for (auto e : task) {
		if (e.second >= en) {
			en = e.first;
			ans++;
		}
	}
}

int main(void) {
	cin >> N;
	for(int i=0; i<N; i++) {
		int st, en;
		cin >> st >> en;

		//끝나는 시간 기준으로 정렬하기 위해 en을 first에 넣음. -> sort에 pair이 들어가면 first를 기준으로 정렬하기 때문
		//불편하다면 greater()비교함수를 직접 짜서 두 번재 인자를 기준으로 설정하면 됨. 하지만 매우 귀찬... 빨리 해결하는게 중요함!
		task[i] = { en, st };
	}
	sort(task, task + N);
	solve();
	cout << ans;
	return 0;
}

두 예제문제에서 알 수 있듯 그리디는 데이터의 정렬 기준이 정말 중요합니다.

 

5. 정리

정리하면 그리디는 일관된 사고로 접근하면서 그럴듯한 최적해를 떠올릴 수 없다면 한번 의심해봐야 합니다. 그리고 그리디를 떠올렸다면 어떤 기준으로 데이터를 정렬, 세팅할지 의심해보고 검증을 통해 구현합니다. 여기서 중요한 것은 데이터의 정렬 기준입니다. 

하지만 실전에서는 일일이 검증할 시간이 없으므로 평소에 완벽하게 검증해보려는 노력을 하고 실전에서는 그냥 풀어야 합니다. "따라서 실전에서는 어떤 기준으로 정렬하면 미래를 고려하지 않고 최적해를 찾을 수 있을까?"를 기준으로 고민해 보는것이 현실적이고 실전적인 풀이 방법입니다. 실전에서 그냥 넘어가려면 평소에 많은 문제를 풀어봐야겠지요?

저는 이것이 그리디적 감각인 것 같습니다.

 

이번 포스팅에서는 그리디에 대해서 다루어 봤습니다. 다른 많은 문제들은 블로그의 그리디 카테고리에서 다룰 예정이니 필요시에 참고하면 좋을 것 같습니다.